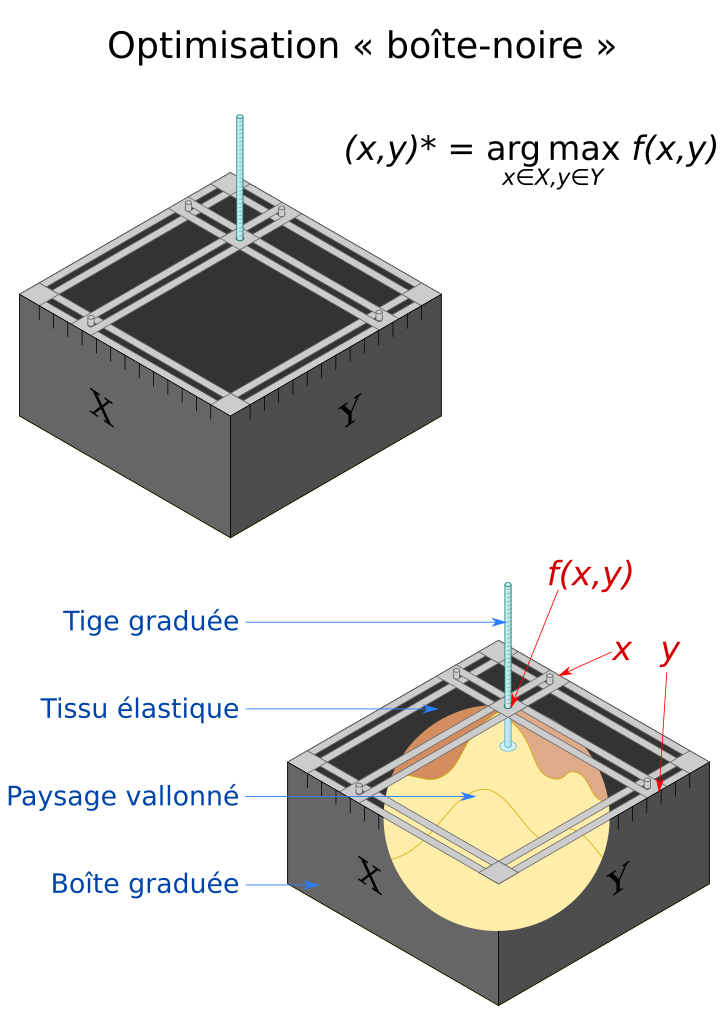
Plan de maquette figurant l'optimisation boîte-noire
Ce projet propose un dispositif permettant d'expliquer de manière simple un problème mathématique au cœur de l'informatique moderne. Le dispositif est manipulable par n'importe qui et permet de mettre en place un jeu heuristique aux implications plus profondes qu'il n'y parait.
L'optimisation mathématique est au cœur des prises de décisions programmées sur ordinateur. Il y a beaucoup de manières de poser un problème d'optimisation, l'un de mes favoris étant le modèle en « boîte-noire ». Dans ce modèle, on cherche à maximiser (ou minimiser, ça ne change rien) une fonction $f:X\to \mathbb{R}$ dont on ne connaît rien sur la forme analytique à part ses bornes ; $x\in X := [x_{\rm min},\,x_{\rm max}]\subset \mathbb{R}^n$. $$x^* = \mathop{\rm arg\,max}_{x\in X} f(x)$$
Ce genre de problème est — d'un point de vue mathématique — presque équivalent au problème qui se poserait à un alpiniste qui chercherait la plus haute montagne d'un massif plongé dans le brouillard le plus opaque.
La seule chose qu'un algorithme d'optimisation puisse faire consiste donc à obtenir la valeur d'une solution et à procéder par essai/erreur afin de trouver celle ayant la meilleure valeur.
Intuitivement, on peut représenter un tel problème — si on considère deux dimensions — par une boîte (noire) au sens le plus littéral. Le dispositif qu'un être humain pourrait manipuler serait alors une sonde graduée, qu'on peut déplacer dans le plan horizontal (pour choisir une solution) avant de la plonger vers le bas (afin d'évaluer la solution).
Ceci donne un problème de la forme: $$(x,y)^* = \mathop{\rm arg\,max}{x\in X, y\in X} f(x,y)$$ avec $f:X^2 \to [x,0]$.
À l'intérieur de la boîte se trouve un paysage de sable fait de creux et de bosses. Le but du jeu est de trouver la plus haute bosse (ou le creux le plus profond), alors qu'on ne voit pas l'intérieur de la boîte, qui est recouvert d'un tissu (élastique). Bien évidemment, vous n'avez qu'un temps limité pour ce faire, et donc un nombre de sondages donné.
Il faut également imaginer qu'on peut poser le problème sur plus de deux dimensions.
Comment procéderiez-vous pour trouver la meilleure solution ?
Commencez déjà par télécharger le fichier SVG source.